![]()
- Rappels sur les grammaires
- Définition d'analyse descendante
- Un exemple simple en Ocaml
- Définition et construction de NULLABLE, FIRST, FOLLOW
- Construction de la table LL(1)
- Transformations de grammaires:
- desambigüation par précédence d'opérateurs
- derecursivisation gauche,
- factorisation a gauche
- Un exemple complet
Rappels sur les grammaires: I
Introduite par Chomsky pour traiter le langage naturel,
une grammaire est un quadruplet ![]() , où:
, où:
-

- est un alphabet fini de
terminaux'',<BR> <DT><STRONG> <IMG WIDTH=22 HEIGHT=27 ALIGN=MIDDLE ALT="tex2html_wrap_inline482" SRC="img4.gif" > </STRONG> <DD> est un ensemble fini de symbolesnon terminaux'', avec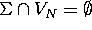
On écrit V pour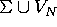 .
.
- S
- est un non terminal distingue nomme le
symbole de départ'' (start symbol'')
-
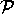
- est une relation finie sur
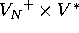 qui définit les
qui définit les règles'' (productions'') de la grammaire.
Une règle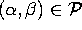 s'écrit aussi
s'écrit aussi 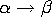 .
.
Rappels sur les grammaires: II
On classifie les grammaires selon la forme de ![]() :
:
- type 0
-
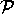 quelconque
quelconque
- type 1
- (contextuelles) pour toute règle
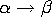 on a
on a 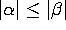 .
.
- type 2
- (libres de contexte) règle de la forme
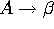 .
.
- type 3
- (rationnelles) règle de la forme
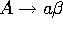 ou
ou 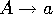 avec a terminal.
avec a terminal.
N.B.: il existent d'autres systèmes de production, comme les L-systems utilisés en biologie.
Rappels sur les grammaires: III
Si ![]() est une règle, on peut alors l'appliquer a n'importe
laquelle séquence
est une règle, on peut alors l'appliquer a n'importe
laquelle séquence ![]() pour obtenir
pour obtenir ![]() et on écrit alors
et on écrit alors
![]()
On écrira ![]() , s'il existent
, s'il existent ![]() , avec
, avec
![]() , t.q.
, t.q. ![]() .
.
Le langage engendre par une grammaire G est
![]()
Résultats fondamentaux:
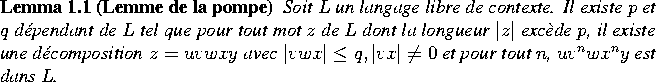
Conséquences:
-
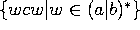 pas libre de contexte
pas libre de contexte
(ex: déclaration avant utilisation des identificateurs) -
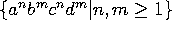 pas libre de contexte
pas libre de contexte
(ex: correspondance entre paramètres formels et actuels d'une procédure) -
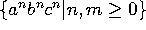 pas libre de contexte
pas libre de contexte
(ex: ancienne technique pour indiquer les mots soulignes)
Arbre de dérivation, ambiguïtés

![]()
Ex: le mot 1+1+1 dans la grammaire
![]()
De façon équivalente, une grammaire est ambiguë si elle permette deux dérivations gauches différentes pour un même mot w.
Backus Naur Form (BNF)
La forme normale de Backus'' est une extension du formalisme des grammaires
libre de contexte qui n'ajoute pas de pouvoir expressif (on ne définit pas une
classe plus large de langages), mais qui permet des définitions plus concises.<BR>
<P>
A la structure des règles on ajoute les notations suivantes:
<P>
<DL ><DT><STRONG>étoile de Kleene</STRONG>
<DD>: on peut écrire <P> <IMG WIDTH=292 HEIGHT=14 ALIGN=BOTTOM ALT="displaymath588" SRC="img30.gif" > <P>
a la place de
<P> <IMG WIDTH=414 HEIGHT=14 ALIGN=BOTTOM ALT="displaymath589" SRC="img31.gif" > <P>
<DT><STRONG>option</STRONG>
<DD>: on peut écrire <P> <IMG WIDTH=293 HEIGHT=20 ALIGN=BOTTOM ALT="displaymath590" SRC="img32.gif" > <P>
a la place de
<P> <IMG WIDTH=405 HEIGHT=14 ALIGN=BOTTOM ALT="displaymath591" SRC="img33.gif" > <P>
<DT><STRONG>cas</STRONG>
<DD>: on peut écrire <P> <IMG WIDTH=322 HEIGHT=20 ALIGN=BOTTOM ALT="displaymath592" SRC="img34.gif" > <P>
a la place de
<P> <IMG WIDTH=276 HEIGHT=71 ALIGN=BOTTOM ALT="displaymath593" SRC="img35.gif" > <P>
</DL>
Bien entendu, il faudra faire attention a ne pas mélanger les symboles BNF
avec les terminaux de <IMG WIDTH=12 HEIGHT=13 ALIGN=BOTTOM ALT="tex2html_wrap_inline480" SRC="img3.gif" > . Dans l'énoncé du projet, par exemple, on a
pris soin de distinguer tout symbole <em>s</em> de <IMG WIDTH=12 HEIGHT=13 ALIGN=BOTTOM ALT="tex2html_wrap_inline480" SRC="img3.gif" > en l'écrivant
'<em>s</em>', comme pour les caractères de Ocaml. Mais s'il n'y a pas
d' ambiguïté, on ne se fatiguera pas a faire la distinction.
<HR><H1><A NAME="SECTION00060000000000000000"> Analyse descendante</A></H1>
<P>
Le problème de l'analyse est celui de prendre une grammaire <I>G</I>, et de
construire un algorithme capable, pour toute chaîne <I>w</I> de terminaux, de décider
si elle appartient ou non a <I>L</I>(<I>G</I>). De plus, on demande de reconstruire un arbre
de dérivation pour <I>w</I> dans <I>G</I> en cas de réponse affirmative.<BR>
<P>
Certains langages permettent de résoudre ce problème a l'aide d'une méthode fort
simple, l'analyse dite <em>descendante</em>.<BR>
<P>
Cette méthode cherche a construire une dérivation gauche directement a partir du
symbole initial, ou de façon équivalente, cherche a construire un arbre de
dérivation a partir de la racine avec une exploration en profondeur d'abord de
gauche a droite.<BR>
<P>
Pour cela, l'analyseur doit pouvoir décider, en s'aidant éventuellement avec
les prochains <I>k</I> symboles en entrée, quelle est la prochaine production dans
la dérivation gauche que l'on reconstruit.<BR>
<P>
Vue ladistance'' entre le terminal que l'on voit en entrée et la production
a choisir, il n'y a pas trop de chance pour que la méthode fonctionne (en
particulier toute grammaire ambiguë posera des problèmes), mais si on réussit,
alors le langage de la grammaire est dans la classe LL(k) (langages
analysables en parcourant l'entrée de gauche (L) a droite et en reconstituant une
dérivation gauche (L)).
Exemple OcamlLex
Voyons un exemple de grammaire LL(1) et un analyseur construit a la main en Ocaml:
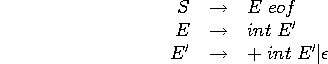
exception Parse_Error;;
type token = Int | PLUS | Eof;;
let descente gettoken =
let tok = ref (gettoken()) in let advance () = tok := gettoken() in
let eat t = if (!tok = t) then advance() else raise Parse_Error in
let check t = if (!tok = t) then () else raise Parse_Error in
let rec ntS () = (ntE(); check(Eof))
and ntE () = match !tok with Int -> (eat(Int); ntE'())
| _ -> raise Parse_Error
and ntE' () = match !tok with PLUS -> (eat(PLUS);eat(Int); ntE'())
| _ -> () ( transition vide )
in ntS();;
( un lexeur bidon vite fait )
let gettoken_of l = let data = ref l in
let f () = let t = List.hd !data in data:= List.tl !data; t in f;;
descente (gettoken_of [Int;PLUS;Int;PLUS;Int;Eof]);;
Analyseurs LL(1): choisir la production en regardant le prochain token
Pour réaliser un analyseur LL(1), il s'agit de remplir une table de la forme
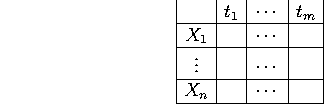
en mettant une règle de production ![]() dans la case
dans la case
![]() si le fait de voir le token
si le fait de voir le token ![]() indique qu'on peut appliquer
la règle de production
indique qu'on peut appliquer
la règle de production ![]() .
.
S'il n'y a pas de cases avec plus d'une entrée une fois le remplissage fini,
on aura réussi et on pourra implémenter l'analyseur.
NULLABLE, FIRST, FOLLOW
comment remplir les cases?
pour cela on a besoin de calculer pour les symboles
de la grammaire trois ensembles:
![]() )
)
![]() dérivable à
partir de X
dérivable à
partir de X
Définition formelle de NULLABLE, FIRST, FOLLOW
On peut voir ces ensembles comme des relations, et alors
- Nullable est la plus petite relation Nu t.q.
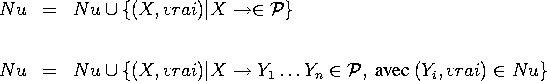
- First est la plus petite relation Fi telle que
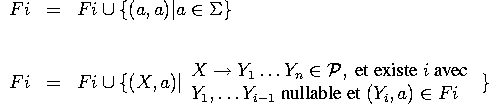
Définition formelle de NULLABLE, FIRST, FOLLOW
Enfin, Follow est la plus petite relation Fo telle que
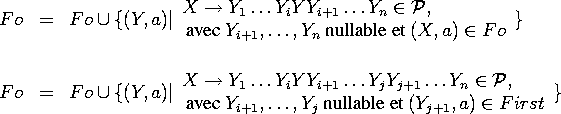
![]()
N.B.: ce qui fait que ce point fixe existe toujours et est atteignable de cette sorte est la continuité (par rapport a une topologie bien choisie) des opérations ensemblistes utilisées dans la définition.
Construction de la table LL(1)
Une fois calcules Nullable(X), First(X) et Follow(X) pour tout symbole, il est facile de calculer aussi Nullable et First sur une séquence de symboles:
- Nullable(
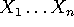 )
)
- est vrai ssi Nullable(
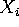 ) est vrai
pour
) est vrai
pour 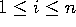 ;
;
- First(
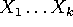 )
)
- est First(
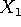 ) si
) si 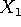 n'est pas nullable
n'est pas nullable
- First(
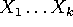 )
)
- est
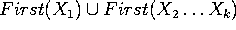 si
si 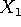 est nullable
est nullable
Et on peut finalement remplir notre table
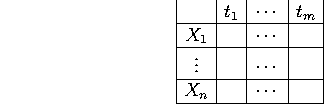
de la façon suivante, on analyse toute production ![]() et
et
- on met
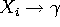 dans la case
dans la case 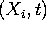 si
si 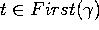
- on met
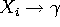 dans la case
dans la case 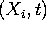 si
si 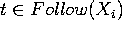 et
et 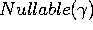
Transformations préliminaires: élimination de l'ambiguïté
L'existence d'une grammaire non ambiguë pour un langage donne L n'est pas
décidable. Cependant, dans les cas les plus fréquents, on sait éliminer
l'ambiguïté assez facilement:
Exemple: on peut réécrire la grammaire (ambiguë)
![]()
en imposant une priorité sur les opérateurs et une associativité, comme:
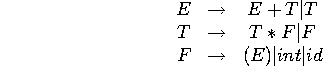
qui reconnaît le même langage, mais n'est pas ambiguë.
Transformations préliminaires: derecursivisation
Une grammaire recursive a gauche pose toujours de problèmes pour LL(1):
si on a deux productions ![]() et
et ![]() ,
alors il y aura toujours une double entrée dans les cases (E,t) pour
,
alors il y aura toujours une double entrée dans les cases (E,t) pour ![]() .
.
Mais on sait éliminer la récursion a gauche de toute grammaire: toute production
![]()
peut être remplacée par les productions (équivalentes, si X' est un symbole nouveau) :
![]()
Transformations préliminaires: factorisation gauche
Un autre exemple de problème pour LL(1) apparaît si on a deux productions
![]() et
et ![]() qui ont le même préfixe
qui ont le même préfixe
![]() : l'analyseur ne saura pas non plus dans ce cas faire le bon choix.
: l'analyseur ne saura pas non plus dans ce cas faire le bon choix.
On sait améliorer la situation en factorisant'' a gauche le préfixe commun: toute
production
<P>
<P> <IMG WIDTH=330 HEIGHT=20 ALIGN=BOTTOM ALT="displaymath726" SRC="img67.gif" > <P>
<P>
peut être remplacée par les productions (équivalentes, si X' est un symbole nouveau) :
<P>
<P> <IMG WIDTH=323 HEIGHT=43 ALIGN=BOTTOM ALT="displaymath727" SRC="img68.gif" > <P>
<P>
<HR><H1><A NAME="SECTION000160000000000000000"> Transformations préliminaires: factorisation gauche, II</A></H1>
<P>
Voyons un exemple bien connu:
<P>
<P> <IMG WIDTH=401 HEIGHT=20 ALIGN=BOTTOM ALT="displaymath738" SRC="img69.gif" > <P>
<P>
devient
<P>
<P> <IMG WIDTH=347 HEIGHT=43 ALIGN=BOTTOM ALT="displaymath739" SRC="img70.gif" > <P>
<P>
N.B.: ce n'est pas LL(1) non plus, mais on sait mieux gérer ce deuxième cas que
le premier (ex. en donnant priorité au caselse'')
Un exemple complet
![]()
On veut analyser
![]()
Cette grammaire est ambiguë, donc nous allons appliquer notre technique de desambiguation.
Un exemple complet: desambiguation
En imposant que * lie plus que + et qu'on associe a gauche, on obtient la grammaire non ambiguë:
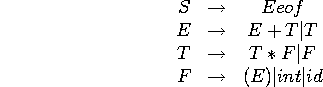
Mais cette grammaire est recursive a gauche, donc ...
Un exemple complet: derecursivisation
En derecursivisant, on arrive a:
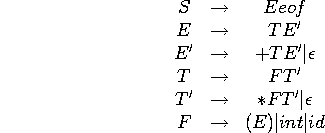
On va maintenant calculer Nullable, First et Follow dans l'ordre
Calcul de Nullable
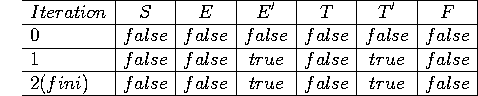
Calcul de First
On sait que :
![]()
On calcule First:

Calcul de Follow
On sait que :
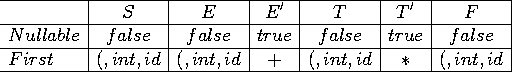
On calcule Follow:
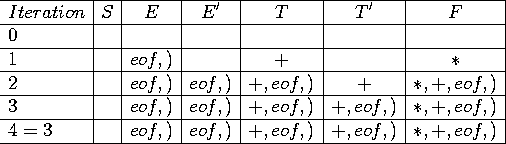
La table de l'automate
On peut finalement construire la table de l'automate: On sait que :
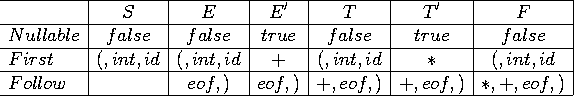
On construit alors:
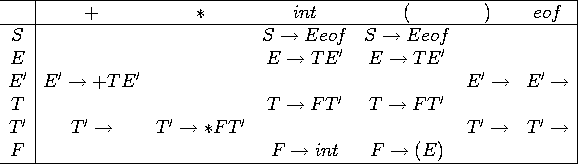
Enfin, notre programme d'analyse en Ocaml
exception Parse_Error;;
type token = Int | PLUS | TIMES | LPAR | RPAR | Eof;;
let descente gettoken =
let tok = ref (gettoken()) in
let advance () = tok := gettoken() in
let eat t = if (!tok = t) then advance() else raise Parse_Error in
let check t = if (!tok = t) then () else raise Parse_Error
in
let rec ntS () = match !tok with
Int -> (ntE(); check(Eof))
| LPAR -> (ntE(); check(Eof))
| _ -> raise Parse_Error
and ntE () = match !tok with
Int -> (ntT(); ntE'())
| LPAR -> (ntT(); ntE'())
| _ -> raise Parse_Error
and ntE' () = match !tok with
PLUS -> (eat(PLUS); ntT(); ntE'())
| RPAR -> () ( transition vide )
| Eof -> () ( transition vide )
| _ -> raise Parse_Error
and ntT () = match !tok with
Int -> (ntF();ntT'())
| LPAR -> (ntF();ntT'())
| _ -> raise Parse_Error
and ntT' () = match !tok with
TIMES -> (eat(TIMES); ntF(); ntT'())
| PLUS -> () ( transition vide )
| RPAR -> () ( transition vide )
| Eof -> () ( transition vide )
| _ -> raise Parse_Error
and ntF () = match !tok with
Int -> (eat(Int))
| LPAR -> (eat(LPAR);ntE();eat(RPAR))
| _ -> raise Parse_Error
in ntS();;
Enfin, notre programme d'analyse en Ocaml, avec traitement d'erreurs
( on assume que l'on nous passe un analyseur lexical gettoken )
exception Parse_Error;;
type token = Int | PLUS | TIMES | LPAR | RPAR | Eof;;
let descente gettoken =
let position = ref 1 and tok = ref (gettoken()) in
let advance () = tok := gettoken(); position := !position+1 in
let eat t = if (!tok = t) then advance() else raise Parse_Error in
let check t = if (!tok = t) then () else raise Parse_Error
in
let perror s = print_string ("Expecting "^s^" at position: ");
print_int !position; print_newline(); raise Parse_Error in
let rec ntS () = match !tok with
Int -> (ntE(); check(Eof))
| LPAR -> (ntE(); check(Eof))
| _ -> perror "int,("
and ntE () = match !tok with
Int -> (ntT(); ntE'())
| LPAR -> (ntT(); ntE'())
| _ -> perror "int,("
and ntE' () = match !tok with
PLUS -> (eat(PLUS); ntT(); ntE'())
| RPAR -> () ( transition vide )
| Eof -> () ( transition vide )
| _ -> perror "+,),eof"
and ntT () = match !tok with
Int -> (ntF();ntT'())
| LPAR -> (ntF();ntT'())
| _ -> perror "int,("
and ntT' () = match !tok with
TIMES -> (eat(TIMES); ntF(); ntT'())
| PLUS -> () ( transition vide )
| RPAR -> () ( transition vide )
| Eof -> () ( transition vide )
| _ -> perror "+,*,),eof"
and ntF () = match !tok with
Int -> (eat(Int))
| LPAR -> (eat(LPAR);ntE();eat(RPAR))
| _ -> perror "int,("
in ntS();;
Un exemple complet, executable.
Cliquez ici pour un exemple complet, avec lexeur produit par OcamlLex.About this document ...
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 Slides01.tex.
The translation was initiated by Roberto Di Cosmo on Wed Nov 3 20:13:20 MET 1999
Roberto Di Cosmo
Wed Nov 3 20:13:20 MET 1999
